Celestial Devourers

Introduction

Before I set the stage with special and general relativity for why black holes exist and have such strange properties, I will take a moment to indulge you in these delightful extraterrestrial curiosities.

So many of you have heard of black holes and are understandably impressed. They are key to star formation within galaxies and we have one at the center of our galaxy. These monsters of the cosmos have such a high concentration of mass that anything going by too close will be pulled in by the curvature of space there. Wait did I just say curvature of space and imply that mass causes it?

Have no worries...
we will soon fill in all these details as the story of black holes unfolds.

Black Hole visualized as a monster. Center of eye represents black hole and white of eye represents plasma.

(On phone/iPad press image for description. On Desktop hover image for description.)

Black Holes Even Eat Light

I also said that anything going by too close will be pulled in, and what is crazy is that this even includes light. Let’s take a minute to put that into perspective and understand light.

Usually, you shine a flashlight on something, say a red apple, and some light gets absorbed and in this case the red light bounces back to your eye and you see the apple.

Well for a black hole, if you shine a flashlight at it, the light crosses over the event horizon, which acts as a point of no return, and the light never comes back to your eyes.

Light hitting red apple and making it visible.

Photo of Black Hole

So now let’s have a look at these images of black holes and see why we know they’re a black hole and not just a smudge of stars.

Simulation and Captured Black Hole.

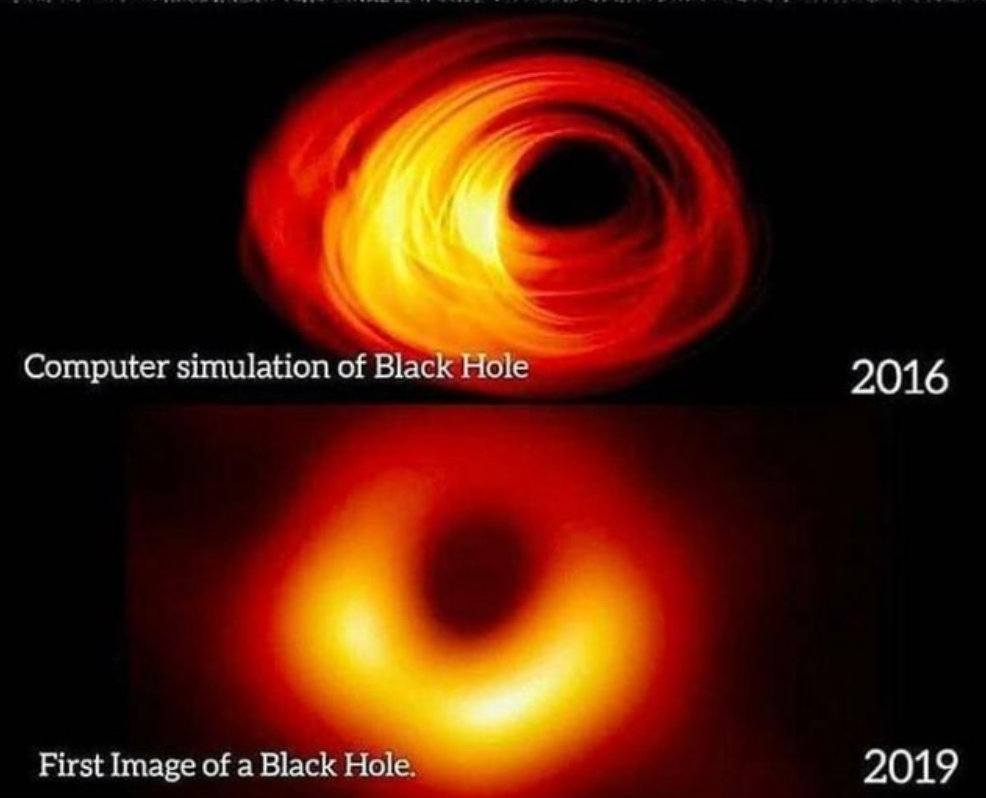
If we look at this dark center we see that this is what is inside the event horizon. The light never bounces back to our telescope, but rather it gets sucked into the black hole.

Meanwhile this ring of orange we see is from particles accelerating so fast they become a plasma - like when you microwave a grape - and emit radio waves that the telescope collects.

Radio waves are on the electromagnetic spectrum with visible light and microwaves and uv light. They have a much longer wavelength and this gets picked up by radio receivers all around the world and computers combine it all together into this beautiful image of a black hole.

Special Relativity

So before we get into the madness of curved space and general relativity, let's talk about special relativity and how Einstein changed our understanding of space and time. First, take a look at the nearest clock in your room that isn't your phone.

What I’m about to say will sound crazy, but if you and your smartphone clock were to jump aboard a super fast spaceship and travel in circles around the earth and come back, the clock in your room may say 6:00 when your smartphone says 5:50.

As you travel faster time slows down and this counter intuitive realization comes from scientists’ realization that light always has the same speed.

As You Travel Faster, Time Slows Down

So how could we arrive at such a crazy result of time slowing down when you speed up?
Well, usually when you are in the back of a moving truck and toss a baseball, from land the baseball appears to have added the speed of the truck.

However it has been observed that light stays the speed of light even in this case. Since it is the same speed in the truck where it covers more distance and out of the truck where it covers less distance, then the distance between each second must be larger for the light on the truck so that it keeps the same observed speed.

Game: Relativity Racer

Press < and > arrows to change speed. Notice how the clock speed changes.

Quick Math

To find out how much time slows down, let's make this a little more precise and do some back-of-the-napkin math...

Let's start with the familiar non-special relativity case. If you observe a man in a clear train holding a ball going by at velocity \(v\), and the man tosses the ball forward with velocity \(u\), the observed velocity of the ball will be \(v+u\).

However, after running multiple precise experiments, we have observed that light does not follow these same rules. When you are in a train traveling at \(v\) and you light a candle with light traveling at \(c\), the speed of light in the forward direction is \(c\), not \(c+v\). This constant speed of light is the basis for the effects of Special Relativity.

This limit of the speed of light leads to another peculiar result. Let's say you are sitting in a tree watching a woman in a clear train passing below you. There is a mirror on the inner side of the train, and the woman sits across from the mirror, perpendicular to the path the train is traveling.

The woman lights a candle, and from your perspective, the light from the candle takes a path of \(v\) to the mirror and back to the woman, traveling at the speed of light. From her perspective, the light traveled in a straight path to the mirror and back at the speed of \(c\).

Both of you observe the light to have the same speed, but you observe the light to have traveled a further distance (\(v\) path versus straight). Since velocity equals \(\frac{{\text{{position}}}}{{\text{{time}}}}\), time equals \(\frac{{\text{{position}}}}{{\text{{velocity}}}}\). The position/velocity (which equals position/\(c\)) observed for the light is larger for you than it is for the woman in the train. Therefore, we see that less time has passed for her compared to you.

We can see by geometry that \(t'\) (her time in the moving frame) \(= \gamma \times t\) (your time in the stationary frame), where \[\gamma = \frac{1}{\sqrt{1 - \left(\frac{v}{c}\right)^2}}\]

Derivation:

We can see that for velocity approaching the speed of light, \(\gamma\) approaches \(1/\) almost 0, which is a large number (meaning that the 1 second of time that passes for the woman in the moving train is larger than your 1 second of time, indicating that they are experiencing less time passing). Meanwhile, for the small velocities of everyday life, \(\gamma\) is 1 (and 1 second is the same for both observers).

Twin Paradox

Due to time slowing down (the distance between ticks of time increasing) as you travel faster, if two identical twins were on earth, and one left in a high speed flying machine and traveled a while and came back (assuming instantaneous deceleration and acceleration for simplicity), upon returning, the twin that traveled would appear younger than the twin that stayed.

So the takeaway so far is that time isn't fixed, but rather a strange coordinate that depends on your speed through the x, y, and z coordinates. We can represent space and time as a fabric of sorts and this prepares us to begin to understand curvature of space.

Test your knowledge! (refresh to redo)

Curvature

So that’s pretty crazy… that time changes based on how fast you move, but Einstein took things a step further with general relativity.

First imaging yourself jumping off a diving board. When you are up high in the air, do you keep going up...
no something pulls you down - gravity.

You appear to take a nice parabola from the leap until you plop in the water. We take it for granted, but here’s the stumper…
what causes gravity?
Well before we answer that we've got to understand curvature of space.

AI visualization of curved space near black holes.

Let’s imagine a balloon and sharpie. Imagine you draw a straight line on this balloon but since the balloon is round the line looks curved.

Building on the concept of curvature, if you were to trace on a globe an airplane's path around the Earth, it follows a circle (called the great circle), which is basically the straight line analog of Euclidean space within spherical trigonometry.

If you have been in a plane, you may recall that, while you were within the plane, you could imagine that you are stationary and the Earth was what was flying by.

Similarly, if you’re on a random planet, you can imagine that you are stationary (moving only through time) and everything else is flying by. As you saw from the section on special relativity, as you travel faster, time slows down, (aka there is more time between each tick on a clock). So, since you are moving relative to other planets, you can just call your time proper time τ. Due to special relativity, this will vary between objects of different speeds.

So now we can visualize a curved space-time surface of some sort, and you could trace a straight path along it with your finger as you did for the globe. A rocket ship could be travel along this geodesic.

And from within the rocket, the rocket man may think he's stationary and the world is what is zooming by. He would see himself as still in x, y, z space and just moving through his "proper time" (which is in the direction in which you traced out his path).

c, the speed of light

So far, we have visualized the movement of apples, and other forms of mass through space-time. Light travels just through space and not through time and is has the speed c. Analogously, a stationary chair doesn't travel through space and travels through time with speed c. This speed c is important... we see that the mass travels through space-time with the speed of c.

Describing Curvature with Math

We see that in flat space with no force, an object travels with an unchanging velocity through space-time. If that flat space has slanted time and position coordinates, we can used an altered Pythagorean’s theorem to describe the velocity magnitude independent of the coordinate system. This altered Pythagorean’s theorem involves 4 numbers that go together in the Metric Tensor that describes the coordinates' curvature or slant.

Altered Pythagorean’s theorem:

$(ds)^2 = g_{00}\, dx^0\, dx^0 + g_{01}\, dx^0\, dx^1 + g_{10}\, dx^1\, dx^0 + g_{11}\, dx^1\, dx^1$

The numbers \(g_{\mu \nu}\) end up being the components of the Metric Tensor. Using Einstein's vector notation and considering that the velocity magnitude is always the speed of light, we can rewrite this as:

$c^2 = g_{\mu \nu}\, v^{\mu}\, v^{\nu}$

If that flat space has curved time and position coordinates, we can describe the change in unit vector orientation along the object's path with Christoffel Symbols \(\Gamma^\alpha_{ \mu \nu}\), which we can get from the Metric Tensor. A group of Christoffel Symbols make a vector that describes how the unit vector orientation changes along the object's path with respect to the coordinates. For 2 dimensions, there are 8 Christoffel Symbols. We can then plug these Christoffel Symbols into a Geodesic Equation that tells us how the mass will continue in a straight path with the velocity magnitude of c, independent of the curvature of the lines defining the coordinate system.

Geodesic Equation:

$\frac{{dv^\alpha}}{{d\tau}} = -\Gamma^\alpha_{ \mu \nu} v^\mu v^\nu$

Sketch showing that one indication of this curvature is that the orientation of a vector after a two-step movement differs depending on the order of those steps.

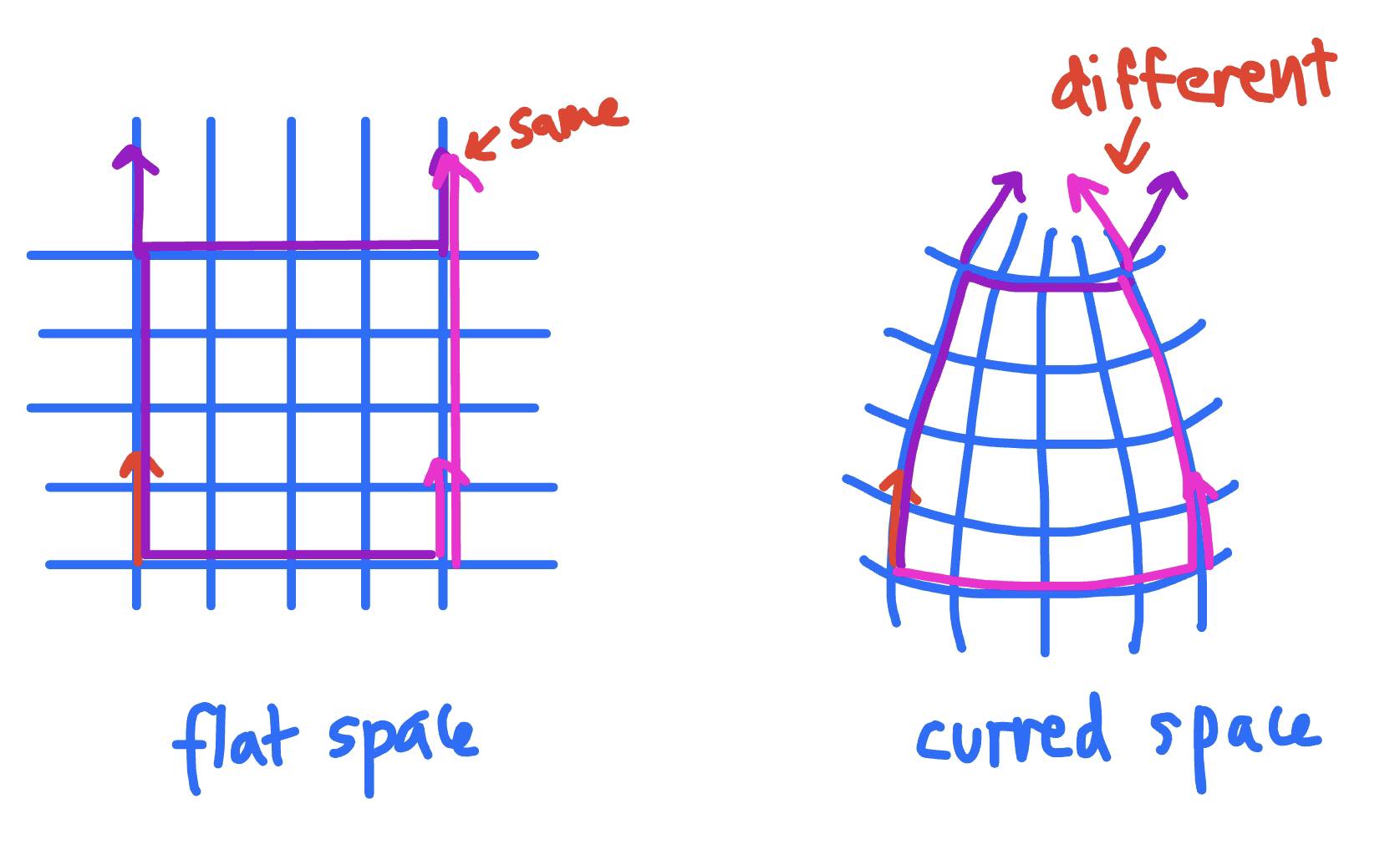
If we look at free space, the Metric Tensor is simply \(c^2\) and -1 across the diagonal and zero in the off-diagonals. (This is called the Minkowski Metric and is used in Special Relativity). The Christoffel Symbols are all zero and the mass’ path is straight. However, we will need to represent space as curved, and one of the signatures of curvature in space is that if you move a vector one way and then the other, your ending orientation is different than if you did this in the opposite order.

Again using 2 dimensions (now imagining a curved surface), the Riemann curvature tensor describes this difference between the two end results using 16 (\(2^4\)) numbers (256 in the case of 4 dimensions) which can be found using the Christoffel Symbols. This giant tensor can be simplified into the Ricci Tensor of 4 numbers, which can be further simplified to the Ricci scalar representing how much parallel lines move apart or together based on the curvature.

Riemann curvature tensor:

$R^\alpha_\beta{}_{\mu \nu} = \frac{d\Gamma^\alpha_{\beta \nu}}{dx^\mu} + \Gamma^\lambda_{\beta \nu} \Gamma^\alpha_{\lambda \mu} - \frac{d\Gamma^\alpha_{\beta \mu}}{dx^\nu} - \Gamma^\lambda_{\beta \mu} \Gamma^\alpha_{\lambda \nu}$

Test your knowledge! (refresh to redo)

General Relativity

But why is this space time surface curved in the first place? What Einstein realized is that the stuff we're made of and the stuff the planets are made of - mass - is all a form of energy that bends space.

Visualization of curved space and lines that travel along it and would be straight in the proper time frame.

Quick Math

To find out how mass and energy relate, let's do some back of the napkin math...

First, we find the fundamental units of energy: \[ J = \text{Nm} = \left(\text{kg}\cdot\text{m/s}^2\right)\cdot\text{m} = \frac{\text{kg}\cdot\text{m}^2}{\text{s}^2} = \frac{\text{M}\cdot\text{L}^2}{\text{T}^2} \]

Next, we use Buckingham Pi and variables of Energy, Mass, and \( c \) to see if there's a relationship.

\[ E = \left(\frac{M \cdot L^2}{T^2}\right) = M \cdot \left(\frac{L}{T}\right)^2 = m \cdot c^2 \]

We get the relationship that energy equals mass times the speed of light squared (a ton of energy is a tiny amount of mass).

What is gravity?

So you think you’re traveling straight like the path a sharpie traces on a balloon, but when you step back and look, you see that you took a curved path (because energy or mass bent space)…
in the case of jumping off a diving board, you took a curved path back to the earth.

Sketch of curved space near mass.

All in all, while it appears that you are traveling in a straight line in the \(\tau\) direction (only through your proper time) from the frame where you are at rest, when you work out what another observer sees you doing, they will see that you are traveling on the curve of space (the geodesic) similarly to how a plane circling earth moves along the great circle, but appears from its frame to move straight.

Where things get even crazier is that time slows down due to curved space...
but we'll talk about that more in a bit.

So in conclusion when you travel fast or near space that is curved due to the presence of energy or mass, time slows down. Gravity is caused by mass or any other type of energy bending space and affecting what path is straight for you.

Test your knowledge! (refresh to redo)

Energy

So mass which is a form of energy \((E=m \times c^2\)) causes curvature of space, but lets dig deeper into this concept of energy.

Visualization of an object falling down a tunnel and changing potential energy into kinetic energy.

Forces may be more straight forward to understand. You can push on something and make it move. While forces are helpful to writing equations to describe the motion of objects, in many situations energy is a more effective tool to get the information you want.

Energy is a quality that is conserved but often changes forms. When an object is moving it has kinetic energy which is \((1/2)mv^2\). This energy can go into friction (rubbing between the surfaces) which results in heat. When an object is up high it has potential energy (\(mgh\)) that turns into kinetic energy when the object is released.

Furthermore, when you calculate kinetic energy of an object minus potential energy it's called the Lagrangian and you can use this as a tool. You can take the time derivative of the partial derivative of this with respect to one derivative of position variable and subtract the partial derivative with respect to that position variable. If you repeat this for every variable that is needed to define an objects position then you get the same equations of motion that you could get with force.

While this sounds like more work, if you use a computer to do the tedious math for you, then you can use energy to get the equations of motion with much less manual rearranging.

Stress Energy Tensor

Now that that framework of understanding how a mass travels through space is established, we can generalize to how gas clouds, the electromagnetic field, dark energy, etc move through space. To do this we can treat everything as a form of energy and just focus on how energy moves through space.

AI Black Hole.

If in 2D you draw an infinitesimal control volume square around point, you can describe the energy flow with the flux through 2 sides (energy conservation gives you the other two sides). These two sides will have flux vectors that make the Energy-Momentum Tensor that describes how momentum is transferred along the different coordinates (energy traveling through time (Energy Density) versus space over time (Momentum Density) versus space (Pressure)).

Generalizing from 2D to our 4D universe, this Stress-Energy Tensor contains 16 components. It has components for energy density, momentum density, pressure, and also viscosity (energy’s tendency to transfer motion to its surroundings). Of course the orientation of your control cube affects the values you get for each of these. When something small like an apple is near a black hole, we can neglect the energy of the apple and treat every component of the Energy-Momentum Tensor as 0.

Now putting all these curvature and energy ideas together, we have discussed tools to describe and work with curved space such as the Ricci scalar and tensor (derived from the Christoffel Symbols), we have discussed using the Metric tensor to describe the curvature of space and how the Pythagorean Theorem is altered, and we have discussed using the Stress-Energy Tensor to look at how mass and other forms of energy move through space.

Now we can use Einstein's Field equation (with the expansion of space added via a cosmological constant) to relate the presence of energy to the curvature of space. We can use this understanding of the curvature of space to understand how the energy continues in a straight path through the very space it bends. \[ R_{\mu \nu} - \frac{1}{2}g_{\mu \nu} R + g_{\mu \nu} \Lambda = \frac{8\pi G}{c^4} T_{\mu \nu} \]

• Ricci Tensor: \(R_{\mu \nu}\)
• Ricci Scalar: \(R\)
• Metric Tensor: \(g_{\mu \nu}\)
• Cosmological Constant: \(\Lambda\)
• Speed of Light: \(c\)
• Newton's Gravitational Constant: \(G\)
• Stress-Energy Tensor: \(T_{\mu \nu}\)

Black Holes

So now we have all the concepts we need to talk about black holes. When the star runs out of nuclear fuel it can collapse under its own weight to become a black hole. The black hole forms as the supernova blows off extra mass and then some of the blown up mass is sucked back in. As for the black hole’s existence, once formed it can gain matter from its surroundings or other black holes or it could continue to loose particles via Hawking radiation until it is gone.

Quick Math

To find out what scales of length and time might be relevant to black holes, let's do some back of the napkin math...

We can use Buckingham Pi to find relationships between relevant variables that can be very telling about our system. Say we have a black hole with mass similar to the mass of our sun (\(2 \times 10^{30}\) kg). Using the speed of light (\(3 \times 10^{8}\) m/s) and G (\(6.67 \times 10^{-11}\) m\(^3\)/kg \(\cdot\) s\(^2\)), we can rearrange our units to get units of length: \[ L = \frac{L^3}{M \cdot T^2} \cdot \left(\frac{T}{L}\right)^2 \cdot M = \frac{G \cdot m}{c^2} \] This gives us a length of about 1500 meters. Looking into the characteristic length, we find that it is the radius of the event horizon (Schwarzschild radius). As we discussed early on, beyond this radius, even light can't escape the black hole's gravitational well.

Next, we rearrange for units of time: \[ T = \frac{(T/L)^3 \cdot L^3}{M \cdot T^2} \cdot M = \frac{G \cdot m}{c^3} \] We get \(5 \times 10^{-6}\) s. Looking into this characteristic time, we find that this is the time it takes for an object to fall into the singularity of a black hole after crossing the event horizon.

Time Near A Black Hole

Time dilation near black holes is a really interesting topic so let’s take a minute to clarify and unpack it.

Black Hole visualized as frozen clock.

Let’s imagine you throw a clock at a black hole. Ignoring spaghettification, you will observe it ticking slower and slower as it gets closer to the black hole. Then when it reaches the event horizon, the clock will appear to be stopped. This is the equation that shows that:

(Where \(\Delta t'\) is the distance between ticks of time near a black hole and \(\Delta t\) is the distance between ticks of time far from a black hole)

But for those of you who like mysteries, time becomes a spatial dimension within the event horizon and we don’t really know how to interpret this. As you know, not even light escapes from inside the event horizon, so we wouldn’t see our clock inside the event horizon at all. Would it still not tick?

Time becomes like space and gets a (+) in front of dt, and what this means is unclear. Another interesting piece of food for thought is that from the clock’s perspective, time is passing normally, and our time is what is sped up, basically to infinity, as it falls past the event horizon.

You may wonder how a black hole could form at all with time slowing to a halt for the supernova mass it's sucking in, so let's clarify this. While the mass that is sucked into the singularity might not be “aging” (like time didn’t pass for it as much as time passed for us watching it from afar), it still traveled through space into the black hole.

Black Hole Pickup Line Generator

LIGO

The "traceless mass quadrupole moment" is a tensor that describes how mass is distributed in space-time. We have discussed how mass distribution affects the curvature of space, but what we haven't discussed is that when this tensor changes, it can send out ripples in space-time known as gravitational waves.

Using conservation of energy, we can assume the energy from the gravitational waves comes from somewhere, but what is the amplitude of a gravitational wave proportional to?

We know these waves are released during black hole merger events. During these events, the 0th moment (mass) is conserved, the 1st moment (\(md\)) is conserved since momentum is conserved. Therefore, the extra energy must come from the 2nd moment (\(md^2\)), which is known as the quadrupole moment.

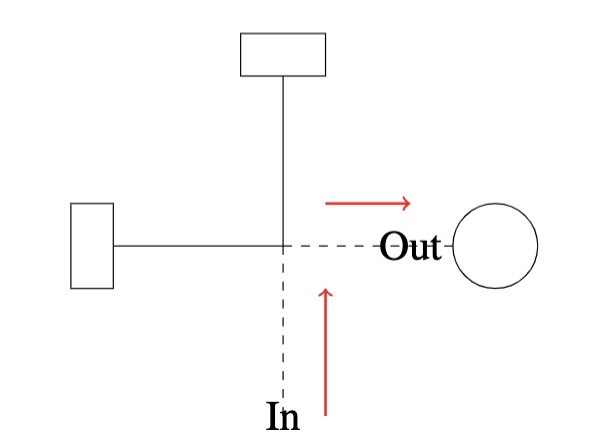
These waves can be detected using a very carefully calibrated measuring tool called LIGO. Along with the photograph, this is one of the ways we are reminded of the presence of black holes. We can watch the simulation or listen to the sound, but essentially, the gravitational waves released when black holes merge increase in a sort of chirp (link).

LIGO basically uses laser beams traveling along two perpendicular lengths with mirrors at the ends and measures whether the lengths are the same by looking at the interference patterns when the two beams are recombined. If a gravitational wave hits, the lengths are changed with respect to each other very slightly, and this creates an interference that is measured.

LIGO's perpendicular arms. Laser path in red. The boxes represent mirrors. The detector is shown as a circle.

Test your knowledge! (refresh to redo)

Conclusions

What a wonderful place to end a story...
with readers more in awe with black holes and the thought scientists and engineers have put into uncovering them than they were when the story started.

Visualization of a black hole as a mysterious little creature.

Through telling the story of black holes we sure have highlighted crazy ways our universe behaves.

As you travel faster time slows down. You can think of space and time as a woven fabric that curves with the presence of energy and mass. This curvature slows time down too. And even light that makes it past the event horizon can not escape the pull of a black hole.

Physics Truth or Dare